В прошлой статье мы рассматривали и даже реализовывали собственноручно такой метод классификации как K ближайших соседей, сегодня будем разбираться с еще одним алгоритмом, название которого — метод опорных векторов (SVM)
Метод опорных векторов (SVM) — это один из наиболее широко используемых алгоритмов машинного обучения в Data Science. SVM используется для решения задач классификации, регрессии и обнаружения выбросов. В этой статье мы рассмотрим SVM как метод классификации.
Что такое метод опорных векторов?
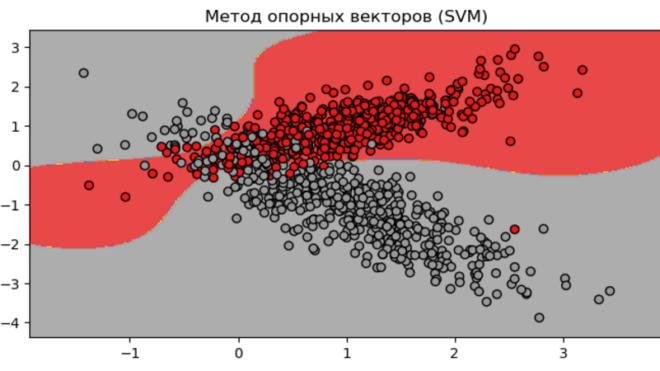
SVM (Support Vector Machines) — это алгоритм машинного обучения, используемый для решения задач классификации, который строит гиперплоскость в n-мерном пространстве для разделения объектов двух или более классов. Гиперплоскость выбирается таким образом, чтобы максимизировать расстояние между гиперплоскостью и ближайшими объектами разных классов (зазор). Объекты, которые расположены ближе всего к гиперплоскости, называются опорными векторами.
Одна из главных идей SVM заключается в том, чтобы преобразовать данные в пространство большей размерности, где объекты могут быть более легко разделены гиперплоскостью. Это достигается через ядро, которое позволяет выполнить нелинейное преобразование данных, сохраняя при этом вычислительную эффективность.
SVM показывает хорошие результаты в задачах классификации, особенно в задачах с большим количеством признаков. Он также может быть эффективен при обучении на небольшом количестве данных.
В функции потерь SVM используется концепция зазора (margin), которая представляет собой расстояние между гиперплоскостью и ближайшими точками разных классов. Цель состоит в том, чтобы максимизировать зазор, при этом допустимо допускать ошибки классификации. Если объекты невозможно разделить линейной гиперплоскостью, то используется мягкая граница (soft margin), которая позволяет допустить ошибки классификации и при этом сохранить разделяющую гиперплоскость.
Для построения SVM используется оптимизационный подход, который заключается в поиске оптимальной гиперплоскости. В общем случае, SVM может быть формализован как задача квадратичного программирования, которая заключается в минимизации функции потерь и максимизации зазора между классами.
SVM является гибким алгоритмом, который позволяет использовать различные ядра для выполнения нелинейного преобразования данных. Классические ядра, такие как линейное, полиномиальное и радиально-базисное, могут быть использованы для преобразования данных в более высокое измерение. Также возможно создание собственных ядер, которые позволяют адаптировать алгоритм SVM к конкретным задачам.
ML Практикум: от теории к промышленному использованию
Код курса
PYML
Ближайшая дата курса
11 августа, 2025
Продолжительность
24 ак.часов
Стоимость обучения
54 000 руб.
Ядра SVM
Метод опорных векторов (SVM) использует ядро (kernel) для преобразования пространства данных, в котором находятся объекты, чтобы разделить их на классы. Ядро определяет функцию сходства между объектами в новом пространстве признаков.
Вот четыре основных ядра, которые мы рассмотрим в нашем примере ниже:
- Линейное ядро (Linear kernel) — это самое простое ядро, которое строит гиперплоскость для разделения данных. Оно часто используется в задачах с линейно разделимыми данными. В математическом смысле линейное ядро вычисляет скалярное произведение между векторами признаков объектов.
- Ядро Radial Basis Function (RBF) — это наиболее распространенное ядро, которое может разделять данные, не являющиеся линейно разделимыми. Оно создает границу принятия решений в виде радиально-симметричного колокола.
- Ядро с полиномиальной функцией (Polynomial kernel) — это ядро, которое вводит полиномиальную функцию в пространство признаков для разделения данных. Это может быть полезно для данных, которые не могут быть разделены гиперплоскостью.
- Ядро с сигмоидной функцией (Sigmoid kernel) — это ядро, которое используется для моделирования нейронных сетей. Оно может работать с нелинейными данными, но не так эффективно, как RBF-ядро.
Каждое ядро может иметь свои параметры, которые могут быть настроены для улучшения производительности модели.
ML Практикум: от теории к промышленному использованию
Код курса
PYML
Ближайшая дата курса
11 августа, 2025
Продолжительность
24 ак.часов
Стоимость обучения
54 000 руб.
Пример применения в Python
Сравним принцип работы описанных выше ядер. Так как реализовать их вручную будет несколько накладно, на этот раз всё же воспользуемся готовым решением из scikit-learn. Для начала нам нужно импортировать необходимые библиотеки и сгенерировать набор данных:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
from sklearn.metrics import accuracy_score
from sklearn.datasets import make_classification
# Генерируем данные для обучения
X, y = make_classification(n_samples=1000, n_features=2, n_redundant=0, n_informative=2,
random_state=1, n_clusters_per_class=1)
Мы знаем, что эти классы не являются линейно разделимыми. Но SVM позволяет нам решить эту проблему, преобразовав данные с помощью ядерного преобразования. Далее обучим отдельную модель для каждого ядра:
# Создаем экземпляр SVM и обучаем модель с использованием линейного ядра
C = 1.0 # параметр регуляризации SVM
linear_svc = svm.SVC(kernel='linear', C=C).fit(X, y)
# Создаем экземпляр SVM и обучаем модель с использованием RBF-ядро
rbf_svc = svm.SVC(kernel='rbf', gamma=0.7, C=C).fit(X, y)
# Создаем экземпляр SVM и обучаем модель с использованием полиномиального ядра
poly_svc = svm.SVC(kernel='poly', degree=2, C=C).fit(X, y)
# Создаем экземпляр SVM и обучаем модель с использованием сигмоидного ядра
sig_svc = svm.SVC(kernel='sigmoid', C=C).fit(X, y)
# оцениваем качество моделей
print('Accuracy of linear kernel:', accuracy_score(y, linear_svc.predict(X)))
print('Accuracy of polynomial kernel:', accuracy_score(y, poly_svc.predict(X)))
print('Accuracy of RBF kernel:', accuracy_score(y, rbf_svc.predict(X)))
print('Accuracy of sigmoid kernel:', accuracy_score(y, sig_svc.predict(X)))
OUT:
Accuracy of linear kernel: 0.898
Accuracy of polynomial kernel: 0.924
Accuracy of RBF kernel: 0.922
Accuracy of sigmoid kernel: 0.815
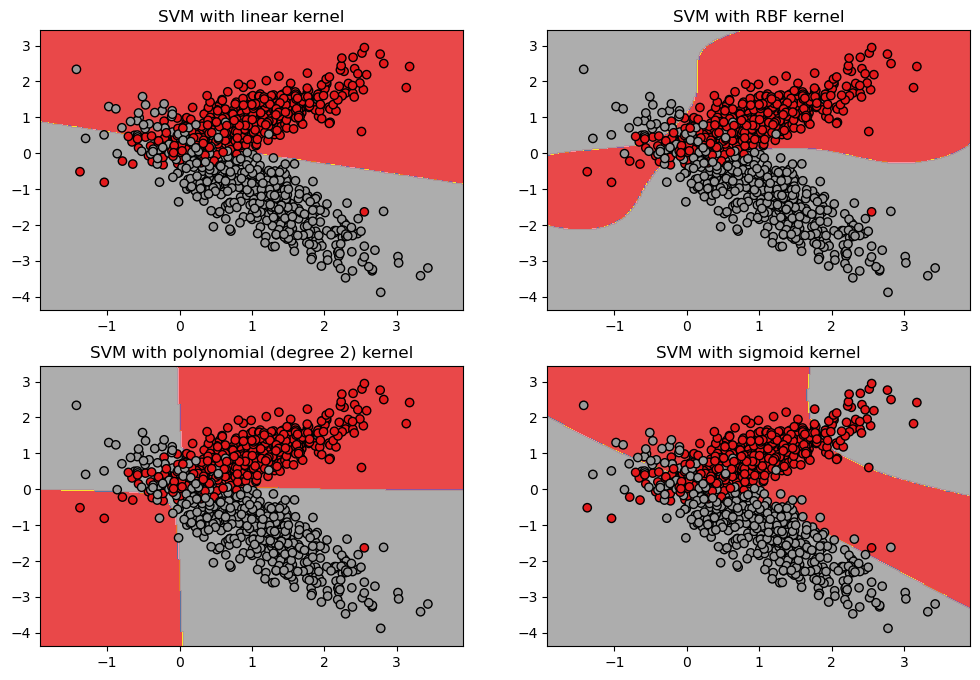
Здесь мы создаем четыре экземпляра SVM, каждый со своим типом ядра (линейное, RBF, полиномиальное и сигмоидное) и обучаем их на наших сгенерированных данных.
Теперь мы можем построить график для каждой из моделей, чтобы увидеть, как они разделяют данные:
# Создаем сетку для графиков
h = 0.02 # шаг в сетке
x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# Заголовки графиков
titles = ['SVM with linear kernel',
'SVM with RBF kernel',
'SVM with polynomial (degree 2) kernel',
'SVM with sigmoid kernel']
# Создаем график
plt.figure(figsize=(12, 8))
for i, clf in enumerate((linear_svc, rbf_svc, poly_svc, sig_svc)):
# Рисуем границы принятия решений на графике
plt.subplot(2, 2, i+1)
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.Set1, alpha=0.8)
# Рисуем точки данных
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1, edgecolor='k')
plt.title(titles[i])
plt.show()
Мы можем видеть, что каждая модель разделяет данные по-разному. Линейная модель (верхний левый угол) строит прямую границу между классами, тогда как модели с нелинейными ядрами строят более сложные границы, чтобы разделить классы.
Это демонстрирует мощь SVM и то, как она может использоваться для решения задач классификации в Python.
ML Практикум: от теории к промышленному использованию
Код курса
PYML
Ближайшая дата курса
11 августа, 2025
Продолжительность
24 ак.часов
Стоимость обучения
54 000 руб.
Преимущества:
- Высокая точность: SVM является одним из наиболее точных алгоритмов машинного обучения, которые могут обучаться на больших наборах данных.
- Хорошая работа с высокоразмерными данными: SVM может хорошо работать с данными, которые имеют большое количество признаков.
- Работает с небольшими выборками данных: SVM может работать с малым количеством данных и хорошо обобщать.
- Малое количество гиперпараметров: SVM имеет только несколько гиперпараметров, что делает его относительно простым для настройки.
Недостатки:
- Чувствительность к шуму: SVM может быть чувствителен к шуму в данных. Шум в данных может привести к тому, что SVM строит границу принятия решений, которая не обобщается хорошо на новые данные.
- Вычислительная сложность: SVM может быть вычислительно сложным для обучения на больших наборах данных.
- Выбор функции ядра: Выбор правильной функции ядра может быть сложной задачей. Некоторые ядра работают лучше на определенных типах данных, и выбор неправильного ядра может привести к плохим результатам.
В целом, SVM — это мощный алгоритм машинного обучения, который может использоваться для решения различных задач классификации и регрессии. Он имеет несколько преимуществ и недостатков, которые необходимо учитывать при выборе алгоритма машинного обучения для конкретной задачи.
Если вам интересно узнать больше о машинном обучении на Python и быть в курсе последних методов и инструментов, мы рекомендуем посетить наш учебный центр, который находится в Москве и специализируется на повышении квалификации ИТ-специалистов. Там вы сможете пройти практический курс «Машинное обучение на Python«.
Источники:
- https://scikit-learn.org/stable/modules/kernel_approximation.html#kernel-approximation