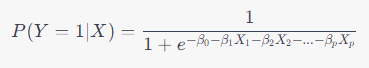В прошлой статье мы говорили о регуляризации, в этой рассмотрим такую линейную модель для решения задачи классификации как логистическая регрессия.
Линейные модели для классификации: логистическая регрессия
В мире Data science задача классификации является одной из самых важных и распространенных задач. Ее основная цель заключается в разделении данных на классы в соответствии с заданными признаками. Линейные модели являются одним из наиболее популярных подходов к решению задачи классификации. В этой статье мы рассмотрим, как использовать линейные модели в Python для решения задачи классификации.
Линейная модель — это математическая модель, которая представляет собой линейную комбинацию входных признаков. В задаче классификации линейная модель используется для разделения данных на два или более классов.
Python предоставляет множество библиотек для работы с линейными моделями. Одна из самых популярных библиотек для работы с линейными моделями в Python — это scikit-learn. Scikit-learn предоставляет множество алгоритмов машинного обучения, в том числе и линейные модели для задачи классификации. Одной из таких моделей является логистическая регрессия.
Логистическая регрессия
Логистическая регрессия — это алгоритм машинного обучения, который используется для решения задачи бинарной классификации, то есть разделения данных на два класса. Она получила свое название благодаря тому, что использует логистическую функцию для прогнозирования вероятности принадлежности объекта к одному из классов.
Логистическая регрессия использует линейную комбинацию входных признаков и соответствующих весов, которая описывает линейную гиперплоскость в пространстве признаков. Затем этот результат проходит через логистическую функцию, которая переводит линейную комбинацию в вероятность принадлежности объекта к одному из классов.
По своей сути логистическая регрессия просто берет уравнение линейной регрессии и использует его как параметр сигмовидной функции. Математически это выражается следующим образом:
где:
Y — бинарный выходной результат (0 или 1)
X — вектор признаков, используемый для прогнозирования $Y$
P(Y=1|X) — вероятность того, что $Y$ равно 1 при заданном $X$
beta_0, beta_1, beta_2, …, beta_p — коэффициенты модели, которые нужно определить в ходе обучения, чтобы достичь наилучшего соответствия данных
e — число Эйлера
Логистическая регрессия также может быть использована для многоклассовой классификации, когда необходимо разделить данные на более чем два класса. Для этого обучают K моделей, каждая из которых отличается только целевым классом. По сути задача бинарной классификации решается несколько раз и выдается совокупное решение нескольких моделей.
В целом, логистическая регрессия — это мощный инструмент для решения задач бинарной и многоклассовой классификации в Python. Она проста в использовании и предоставляет множество метрик для оценки качества работы модели.
ML Практикум: от теории к промышленному использованию
Код курса
PYML
Ближайшая дата курса
11 августа, 2025
Продолжительность
24 ак.часов
Стоимость обучения
54 000 руб.
Реализация цикла обучения логистической регрессии в Python
Реализуем цикл обучения логистической регрессии используя Python. В этом нам снова поможет PyTorch. Для начала импортируем все библиотеки которые нам в этом пригодятся:
import torch import torch.nn as nn import torch.optim as optim import numpy as np from sklearn.datasets import make_classification from sklearn.metrics import classification_report
Далее напишем класс реализующий логистическую регрессию. Прошу обратить внимание, что от линейной регрессии, которую мы реализовывали в ряде предыдущих статей, отличает лишь применение сигмоиды и новый метод predict (так как теперь мы решаем задачу классификации).
class LogisticRegression(nn.Module):
def __init__(self, input_size):
super().__init__()
self.weights = nn.Parameter(torch.randn(input_size, 1))
self.sigmoid = nn.Sigmoid()
def forward(self, x):
x = x @ self.weights
x = self.sigmoid(x)
return x
def fit(self, X, y, lr=0.01, num_iterations=1000):
X = torch.from_numpy(X).float()
y = torch.from_numpy(y).float().view(-1, 1)
# Инициализируем функцию потерь и оптимизатор
criterion = nn.BCELoss()
optimizer = optim.SGD(self.parameters(), lr=lr)
for epoch in range(num_iterations):
# Зануляем градиенты
optimizer.zero_grad()
# Получаем предсказания модели и вычисляем функцию потерь
y_pred = self(X)
loss = criterion(y_pred, y)
# Обновляем веса
loss.backward()
optimizer.step()
def predict(self, X):
X = torch.from_numpy(X).float()
# Получаем предсказания модели и присваиваем метки классов на основе вероятности
y_pred = self(X)
y_pred_labels = [1 if i > 0.5 else 0 for i in y_pred.detach().numpy().flatten()]
return y_pred_labels
На этот раз сгенерируем выборку для классификации самостоятельно, используя make_classification из библиотеки scikit-learn. А далее обучим нашу модель и оценим её качество:
# Генерируем данные
X, y = make_classification(n_samples=1000, n_features=2, n_redundant=0, n_informative=2,
random_state=1, n_clusters_per_class=1)
# Создаем экземпляр класса и обучаем на обучающей выборке
model = LogisticRegression(X.shape[1])
model.fit(X, y, lr=0.1, num_iterations=100)
# Прогнозируем метки классов на тестовой выборке
y_pred = model.predict(X)
print(classification_report(y, y_pred))
OUT:
precision recall f1-score support
0 0.85 0.96 0.90 500
1 0.95 0.83 0.88 500
accuracy 0.89 1000
macro avg 0.90 0.89 0.89 1000
weighted avg 0.90 0.89 0.89 1000
Для чистоты эксперимента обучим логистическую регрессию из библиотеки scikit-learn и увидим, что качество полученных моделей примерно одинаково:
from sklearn.linear_model import LogisticRegression
model = LogisticRegression()
model.fit(X, y)
y_pred = model.predict(X)
print(classification_report(y, y_pred))
OUT:
precision recall f1-score support
0 0.90 0.90 0.90 500
1 0.90 0.90 0.90 500
accuracy 0.90 1000
macro avg 0.90 0.90 0.90 1000
weighted avg 0.90 0.90 0.90 1000
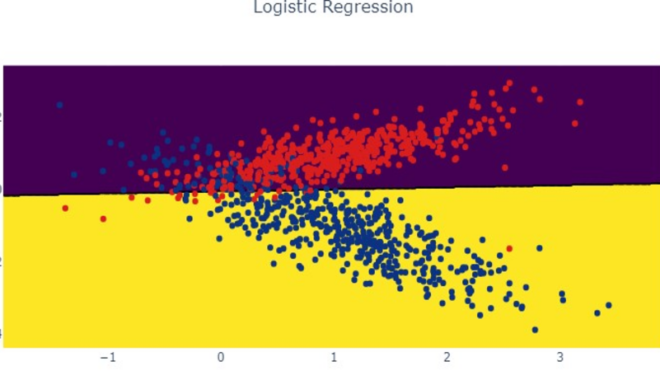
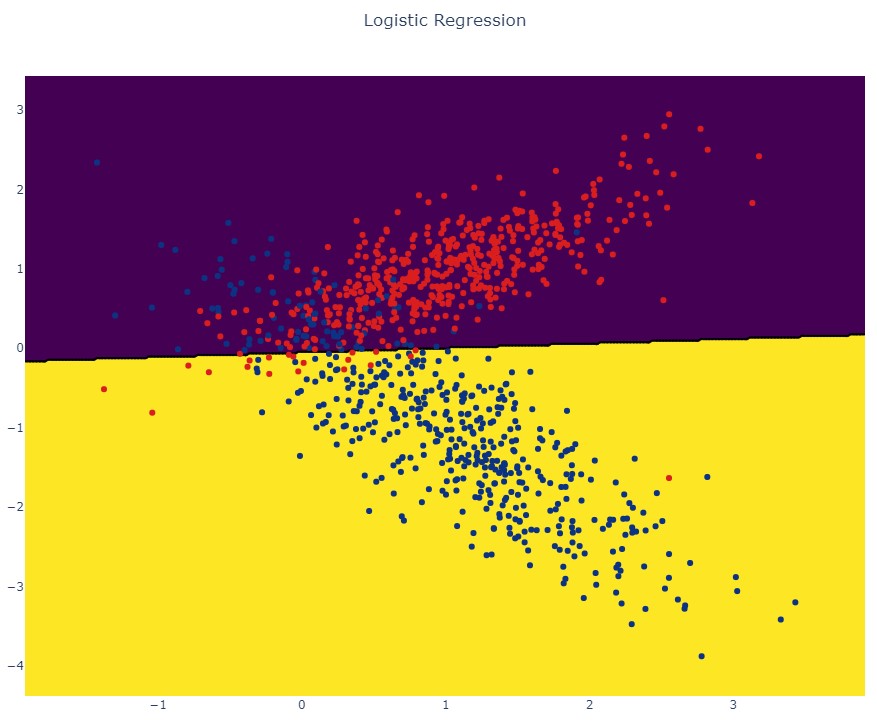
Далее давайте визуально оценим как модель принимает свое решение:
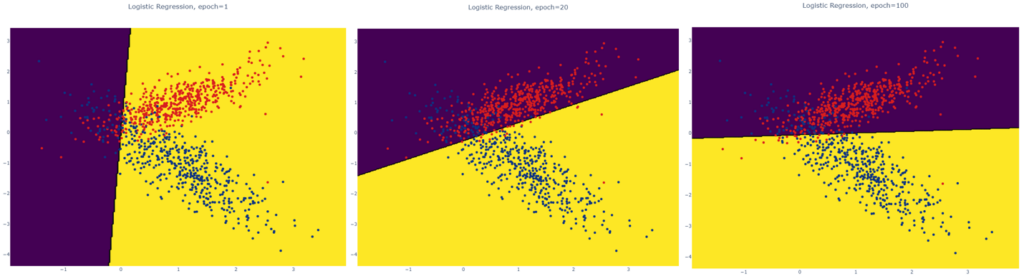
Как видим, результатом работы алгоритма выступает линия разделяющая классы. Если бы мы визуализировали модель в процессе обучения градиентным спуском, то увидели бы как эта линия подбирается в процессе оптимизации:
ML Практикум: от теории к промышленному использованию
Код курса
PYML
Ближайшая дата курса
11 августа, 2025
Продолжительность
24 ак.часов
Стоимость обучения
54 000 руб.
Плюсы логистической регрессии:
- Это относительно простой алгоритм, который требует небольшого количества вычислительных ресурсов и может быть эффективно использован для решения большого количества задач классификации.
- Интерпретируемость: логистическая регрессия позволяет понимать, какие переменные влияют на классификацию и каким образом.
- Работает хорошо на небольших наборах данных: логистическая регрессия показывает хорошие результаты на небольших наборах данных.
- Небольшая вероятность переобучения: логистическая регрессия склонна к менее переобучению, поскольку она не имеет множества параметров, которые нужно оптимизировать.
Минусы логистической регрессии:
- Требуется нормализация признаков: логистическая регрессия требует нормализации признаков, чтобы гарантировать, что признаки вносят одинаковый вклад в модель.
- Работает плохо на сложных задачах: может работать плохо на задачах с большим количеством признаков или сложной структурой данных.
- Линейность: логистическая регрессия работает только с линейными границами решений, что ограничивает ее способность решать сложные задачи классификации.
- Низкая точность: логистическая регрессия может показывать низкую точность, если классы не являются линейно разделимыми.
Если вы хотите узнать больше о машинном обучении на Python и быть в курсе новейших методов и инструментов, мы рекомендуем посетить наш лицензированный учебный центр в Москве, который специализируется на повышении квалификации ИТ-специалистов. Там вы сможете пройти практические курсы «Машинное обучение на Python«.
Источники:
- https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html