В прошлой статье мы рассматривали и даже реализовывали собственноручно такой метод классификации как метод опорных векторов (SVM), сегодня будем разбираться с еще одним весьма популярным алгоритмом – дерево решений (DecisionTree).
Что такое дерево решений?
Дерево решений (DecisionTree) — это модель машинного обучения, которая представляет собой дерево с узлами и листьями. Узлы дерева представляют собой решения, которые необходимо принимать, а листья — конечные результаты. В задачах классификации каждый лист дерева соответствует определенному классу, а в задачах регрессии — числовому значению.
Основная идея алгоритма заключается в построении бинарного дерева, в котором каждый внутренний узел представляет собой условие на признаках, а листья — конечный результат работы алгоритма (например, принадлежность к определенному классу).
Построение дерева происходит по следующему алгоритму:
- Выбирается признак, по которому происходит разделение выборки.
- Выбирается пороговое значение для этого признака.
- Разделяется выборка на две части: объекты, у которых значение признака меньше или равно порогу, и объекты, у которых значение признака больше порога.
- Для каждой из двух полученных подвыборок рекурсивно повторяются шаги 1-3, пока не будет достигнут критерий останова (например, глубина дерева, количество объектов в листе и т.д.).
- В листе дерева выводится ответ — класс или значение целевой переменной.
Выбор признака для разделения может происходить по различным критериям, например, критерию информативности (Information Gain), Gini impurity или энтропии (Entropy). Эти критерии оценивают «чистоту» подвыборок, которые получаются после разделения, и на основании этого выбираются наилучший признак и пороговое значение.
После построения дерева можно использовать его для классификации или регрессии новых объектов, просто проходя по дереву от корня до листа и возвращая значение, которое находится в листе.
DecisionTree — это один из наиболее простых и интерпретируемых алгоритмов машинного обучения, который может быть использован для решения различных задач, например, прогнозирования кредитного скоринга, диагностики заболеваний, определения температуры на улице и т.д.
ML Практикум: от теории к промышленному использованию
Код курса
PYML
Ближайшая дата курса
30 марта, 2026
Продолжительность
24 ак.часов
Стоимость обучения
66 000 руб.
Реализация дерева решений на Python
Теперь давайте попробуем обучить такое дерево сами. Для начала импортируем все нужные нам библиотеки:
import numpy as np import matplotlib.pyplot as plt from sklearn import svm, datasets from sklearn.metrics import accuracy_score from sklearn.datasets import make_classification from sklearn.metrics import classification_report from sklearn.tree import DecisionTreeClassifie rimport graphviz
Конечная реализация Decision Tree зависит от конкретной задачи классификации, поэтому я предоставлю основной каркас, который можно использовать для построения различных моделей деревьев решений.
Ниже приведена реализация классификатора DecisionTree на Python:
class Node:
def __init__(self, feature_idx=None, threshold=None, left=None, right=None, value=None):
self.feature_idx = feature_idx # индекс признака, по которому разбивается вершина
self.threshold = threshold # пороговое значение, по которому разбивается вершина
self.left = left # левое поддерево
self.right = right # правое поддерево
self.value = value # значение в листовой вершине
class DecisionTree:
def __init__(self, min_samples_split=2, max_depth=100, n_feats=None):
self.min_samples_split = min_samples_split # минимальное количество выборок, необходимых для разделения вершины
self.max_depth = max_depth # максимальная глубина дерева
self.n_feats = n_feats # количество признаков, используемых для разделения вершин
self.root = None
def fit(self, X, y):
self.n_feats = X.shape[1] if not self.n_feats else min(self.n_feats, X.shape[1])
self.root = self._grow_tree(X, y)
def _grow_tree(self, X, y, depth=0):
n_samples, n_features = X.shape
n_labels = len(np.unique(y))
# Проверяем условие остановки рекурсии
if (depth >= self.max_depth or n_labels == 1 or n_samples < self.min_samples_split):
leaf_value = self._most_common_label(y)
return Node(value=leaf_value)
feat_idxs = np.random.choice(n_features, self.n_feats, replace=False)
# Ищем лучшее разделение признака
best_feat, best_thresh = self._best_criteria(X, y, feat_idxs)
# Разделяем данные и делаем рекурсивный вызов для левого и правого поддеревьев
left_idxs, right_idxs = self._split(X[:, best_feat], best_thresh)
left = self._grow_tree(X[left_idxs, :], y[left_idxs], depth+1)
right = self._grow_tree(X[right_idxs, :], y[right_idxs], depth+1)
# Возвращаем новую вершину дерева
return Node(best_feat, best_thresh, left, right)
def _best_criteria(self, X, y, feat_idxs):
best_gain = -1
split_idx, split_thresh = None, None
for feat_idx in feat_idxs:
X_column = X[:, feat_idx]
thresholds = np.unique(X_column)
for threshold in thresholds:
gain = self._information_gain(y, X_column, threshold)
if gain > best_gain:
best_gain = gain
split_idx = feat_idx
split_thresh = threshold
return split_idx, split_thresh
def _information_gain(self, y, X_column, split_thresh):
# Вычисляем энтропию перед разбиением
parent_entropy = self._entropy(y)
# Разделяем выборки по пороговому значению
left_idxs, right_idxs = self._split(X_column, split_thresh)
# Если разделение не привело к изменению выборок, возвращаем нулевой информационный прирост
if len(left_idxs) == 0 or len(right_idxs) == 0:
return 0
# Вычисляем энтропию после разбиения
n = len(y)
n_l, n_r = len(left_idxs), len(right_idxs)
e_l, e_r = self._entropy(y[left_idxs]), self._entropy(y[right_idxs])
child_entropy = (n_l / n) * e_l + (n_r / n) * e_r
# Вычисляем информационный прирост
ig = parent_entropy - child_entropy
return ig
def _entropy(self, y):
# Вычисляем энтропию выборки
_, counts = np.unique(y, return_counts=True)
probs = counts / len(y)
entropy = -np.sum(probs * np.log2(probs))
return entropy
def _split(self, X_column, split_thresh):
# Разделяем выборки по пороговому значению
left_idxs = np.argwhere(X_column <= split_thresh).flatten()
right_idxs = np.argwhere(X_column > split_thresh).flatten()
return left_idxs, right_idxs
def _most_common_label(self, y):
# Возвращает наиболее часто встречающееся значение в выборке
_, counts = np.unique(y, return_counts=True)
return max(zip(_, counts), key=lambda x: x[1])[0]
def predict(self, X):
# Прогнозируем метки для новых данных
return np.array([self._traverse_tree(x, self.root) for x in X])
def _traverse_tree(self, x, node):
if node.value is not None:
return node.value
if x[node.feature_idx] <= node.threshold:
return self._traverse_tree(x, node.left)
else:
return self._traverse_tree(x, node.right)
def visualize_tree(self):
# Создаем объект `Digraph` из библиотеки graphviz
dot = graphviz.Digraph()
# Внутренняя функция `add_nodes` для рекурсивного добавления узлов дерева
def add_nodes(node):
# Если узел содержит значение (лист), добавляем его значение в качестве метки
# Иначе добавляем условие разбиения (порог и номер признака)
if node.value is not None:
label = str(node.value)
else:
label = "X[" + str(node.feature_idx) + "] <= " + str(node.threshold)
# Добавляем узел в объект `Digraph`
dot.node(str(id(node)), label)
# Если у узла есть левый потомок, добавляем ребро и вызываем `add_nodes` для левого потомка
if node.left is not None:
dot.edge(str(id(node)), str(id(node.left)))
add_nodes(node.left)
# Если у узла есть правый потомок, добавляем ребро и вызываем `add_nodes` для правого потомка
if node.right is not None:
dot.edge(str(id(node)), str(id(node.right)))
add_nodes(node.right)
# Вызываем `add_nodes` для корневого узла дерева
add_nodes(self.root)
# Возвращаем объект `Digraph`
return dot
Этот код представляет собой реализацию алгоритма дерева решений для классификации. Основным классом является DecisionTree, а узлы дерева представлены классом Node.
Метод init класса DecisionTree инициализирует минимальное количество образцов, необходимых для разделения узла (min_samples_split), максимальную глубину дерева (max_depth), количество признаков для рассмотрения при поиске лучшего разделения (n_feats) и корень дерева (root).
Метод fit класса DecisionTree обучает дерево на входных данных, выращивая дерево рекурсивно с помощью метода _grow_tree.
Метод _grow_tree выполняет следующие шаги рекурсивно:
- Он проверяет, достигнута ли максимальная глубина, есть ли только один метка в данных или количество образцов меньше минимального, необходимого для разделения (min_samples_split). Если хотя бы одно из этих условий выполнено, создается листовой узел с наиболее распространенной меткой данных и возвращается.
- Выбирается подмножество признаков случайным образом, и лучший признак и порог находятся с помощью метода _best_criteria.
- Данные разделяются с использованием лучшего признака и порога, и рекурсивно вызывается метод _grow_tree для левого и правого подмножеств.
- Создается новый узел с лучшим признаком, порогом, левым и правым узлами и возвращается.
Метод _best_criteria ищет лучший признак и порог, перебирая выбранные признаки и пороги и вычисляя информационный выигрыш для каждой комбинации. Возвращаются признак и порог, которые дают наибольший прирост информации.
Метод _information_gain вычисляет информационный выигрыш при разделении с использованием заданного признака и порога. Сначала вычисляется энтропия данных до разделения (parent_entropy). Затем данные разделяются с использованием порога, и вычисляется энтропия данных после разделения (child_entropy). Информационный выигрыш — это мера, которая используется для оценки того, насколько хорошо разделение данных по определенному признаку уменьшает неопределенность в классификации. Информационный выигрыш вычисляется как разница между энтропией до и после разделения данных.
Метод _entropy вычисляет энтропию набора данных.
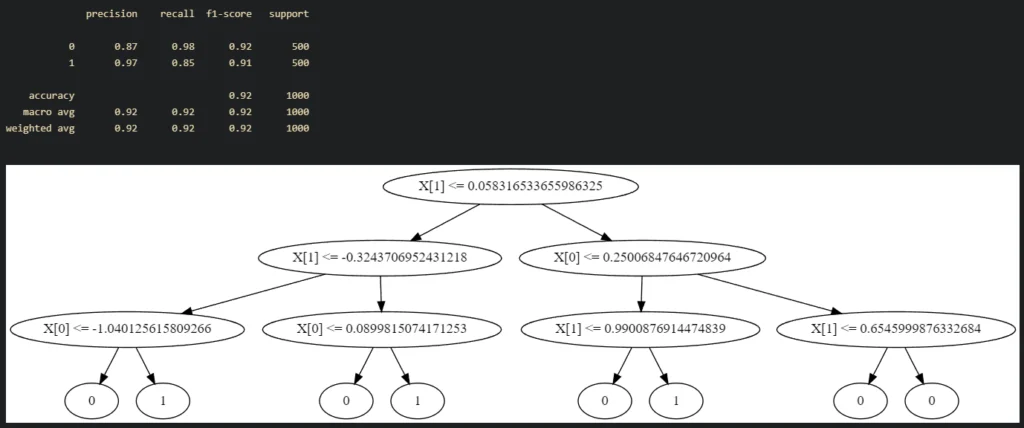
Метод visualize_tree использует рекурсию для обхода узлов дерева и добавляет их в объект Digraph из библиотеки graphviz. Для каждого узла определяется метка, которая представляет собой значение узла (для листьев) или условие разбиения (для узлов-решений). Затем для каждого узла добавляются соответствующие ребра к его потомкам, и рекурсивно вызывается функция add_nodes для каждого потомка. В результате мы получаем визуализацию дерева в виде графа.
ML Практикум: от теории к промышленному использованию
Код курса
PYML
Ближайшая дата курса
30 марта, 2026
Продолжительность
24 ак.часов
Стоимость обучения
66 000 руб.
Теперь давайте обучим наше дерево решений и оценим его качество, а так же визуализируем его:
# Генерируем данные для обучения
X, y = make_classification(n_samples=1000, n_features=2, n_redundant=0, n_informative=2,
random_state=1, n_clusters_per_class=1)
clf = DecisionTree(max_depth=3)
clf.fit(X, y)
# Прогнозируем метки классов на тестовой выборке
y_pred = clf.predict(X)
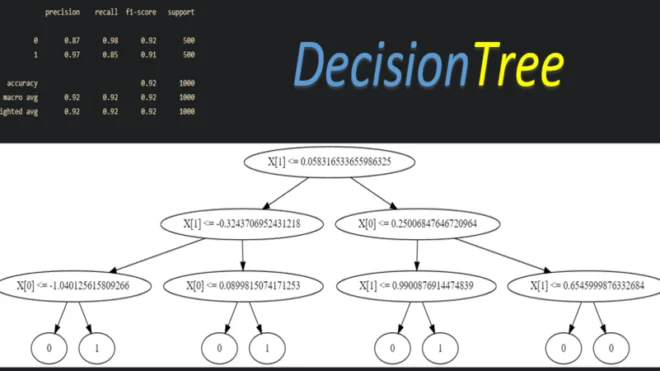
print(classification_report(y, y_pred))
clf.visualize_tree()
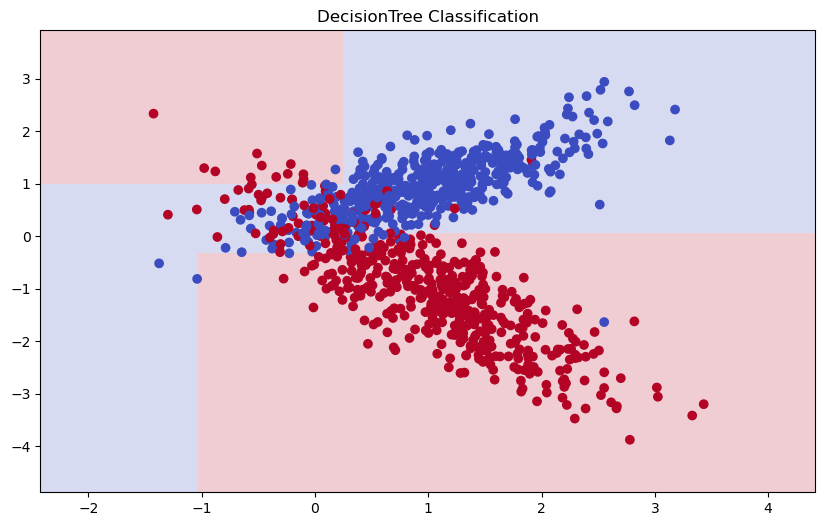
Далее посмотрим какую границу наше дерево построило между классами:
# Plot the decision boundary
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
np.arange(y_min, y_max, 0.02))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.figure(figsize=(10,6))
plt.pcolormesh(xx, yy, Z, cmap='coolwarm', alpha=0.2)
# Plot the data points
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='coolwarm')
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.title("DecisionTree Classification")
plt.show()
Кроме простоты и интерпретируемости, DecisionTree также имеет ряд преимуществ перед другими алгоритмами машинного обучения:
- Может работать с данными различных типов (категориальные, бинарные, числовые)
- Может работать с несбалансированными данными
- Может использоваться для отбора признаков
Однако у DecisionTree также есть некоторые недостатки:
- Склонен к переобучению (overfitting) при большой глубине дерева или при отсутствии ограничений на минимальное количество объектов в листе
- Неустойчив к шуму в данных
- Не гарантирует наилучшее решение, так как выбор оптимального разделения происходит на каждом шаге по отдельности, а не глобально
Чтобы избежать переобучения и улучшить качество работы алгоритма, можно использовать различные техники, такие как:
- Ограничение глубины дерева
- Ограничение минимального числа объектов в листе
- Применение ансамблевых методов, таких как случайный лес (Random Forest)
В целом, DecisionTree — это один из наиболее простых и мощных алгоритмов машинного обучения, который может быть использован для решения широкого спектра задач. Его простота и интерпретируемость позволяют понимать, как работает модель и делать выводы на основе полученных результатов.
ML Практикум: от теории к промышленному использованию
Код курса
PYML
Ближайшая дата курса
30 марта, 2026
Продолжительность
24 ак.часов
Стоимость обучения
66 000 руб.
Если вы заинтересованы в изучении машинного обучения на языке Python и хотите быть в курсе последних методов и инструментов, мы рекомендуем посетить наш лицензированный учебный центр в Москве, который специализируется на обучении ИТ-специалистов. Там вы сможете пройти практический курс «Машинное обучение на Python«.
Источники:
- https://scikit-learn.org/stable/modules/tree.html