Data science не только про обучении ML-моделей. В первую очередь, стоит понять данные: оценить взаимосвязи между переменными, определить их значимость и репрезентативность. Статистика – ключ к раскрытию ваших данных. В этой статье мы поговорим о статистике в Python, какие существуют библиотеки, и как их применять на реальных данных.
Датасет и Pandas для статистического анализа
В качестве анализа возьмем датасет c моллюсками вида abalone, доступный на сайте Kaggle — онлайн-площадке соревнований по машинному обучению. Датасет содержит физические параметры моллюсков: рост, диаметр, высоту, вес раковины и т.д. Также присутствует один категориальный признак — пол моллюска. Ключевым атрибутам является количество колец у моллюска, определяющего его возраст.
Для чтения данных будем использовать pandas. C основами работы pandas вы можете ознакомиться тут.
import pandas as pd
data = pd.read_csv('abalone.csv')
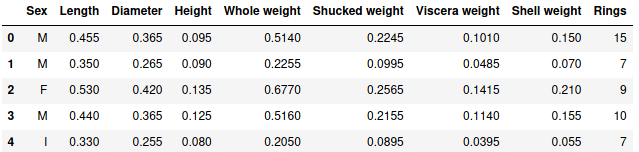
data.head()
Первые строчки выглядят следующим образом:
Описательная статистика в Pandas
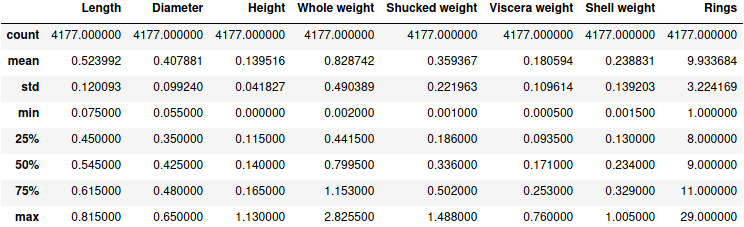
Первое, что можно сделать с предоставленными данными, это посмотреть количество наблюдений, среднее, стандартное отклонение, максимальное и минимальное значения. Python-библиотека Pandas включает метод describe, который позволяет взглянуть на описательную статистику числовых данных:
data.describe()
Результатом является соответствующая таблица:
Проверка на нормальность в Scipy
Нормальный закон распределения является простым и удобным для дальнейшего исследования. Чтобы проверить имеет ли тот или иной атрибут нормальное распределение, можно воспользоваться двумя критериями Python-библиотеки scipy с модулем stats. Модуль scipy.stats поддерживает большой диапазон статистических функций, полный перечень которых представлен в официальной документации.
В основе проверки на “нормальность” лежит проверка гипотез. Нулевая гипотеза – данные распределены нормально, альтернативная гипотеза – данные не имеют нормального распределения.
Проведем первый критерий Шапиро-Уилк [1], возвращающий значение вычисленной статистики и p-значение. В качестве критического значения в большинстве случаев берется 0.05. При p-значении меньше 0.05 мы вынуждены отклонить нулевую гипотезу.
Проверим распределение атрибута Rings, количество колец:
import scipy
stat, p = scipy.stats.shapiro(data['Rings']) # тест Шапиро-Уилк
print('Statistics=%.3f, p-value=%.3f' % (stat, p))
alpha = 0.05
if p > alpha:
print('Принять гипотезу о нормальности')
else:
print('Отклонить гипотезу о нормальности')
В результате мы получили низкое p-значение и, следовательно, отклоняем нулевую гипотезу:
Statistics=0.931, p-value=0.000 Отклонить гипотезу о нормальности
Второй тест по критерию согласия Пирсона [2], который тоже возвращает соответствующее значение статистики и p-значение:
stat, p = scipy.stats.normaltest(data['Length']) # Критерий согласия Пирсона
print('Statistics=%.3f, p-value=%.3f' % (stat, p))
alpha = 0.05
if p > alpha:
print('Принять гипотезу о нормальности')
else:
print('Отклонить гипотезу о нормальности')
Этот критерий также отвергает нулевую гипотезу о нормальности распределения колец у моллюсков, так как p-значение меньше 0.05:
Statistics=242.159, p-value=0.000 Отклонить гипотезу о нормальности
Оценка уровня статистической значимости
T-тест (или тест Стьюдента) решает задачу доказательства наличия различий средних значений количественной переменной в случае, когда имеются лишь две сравниваемые группы. Модуль stats Python-библиотеки scipy также предоставляет t-тест. Стоит заметить, проводить t-тест стоит только в случае нормального распределения анализируемых данных. Для экономии времени и места мы опустим эту часть. Здесь имеется функция ttest_ind, вычисляющую t-тест двух независимых выборок. Для зависимых выборок используется функция ttest_rel.
Рассмотрим атрибут Length (длина моллюска). Разделим генеральную совокупность на две выборки и определим гипотезы. Нулевая гипотеза – средние двух выборок равны, альтернативная гипотеза – средние двух выборок не равны. Проведем тестирование:
half = len(data['Length']) / 2 sam1 = data.loc[:half, 'Length'] sam2 = data.loc[half:, 'Length'] scipy.stats.ttest_ind(sam2, sam1)
Результатом является значение t-статистики и p-значение:
Ttest_indResult(statistic=1.5565212835974083, pvalue=0.11965998094160571)
Как видим, p-значение больше 0.05, что говорит о верности нулевой гипотезы. Кроме того, необходимо проверить, не превышает ли вычисленная t-статистика табличную. Для этого в качестве доверительного интервала выберем 95%. В модуле stats можно посмотреть табличное значение благодаря функции t.ppf. Она принимает в качестве аргументов соответствующие квартили (с доверительным интервалом 95% они будет равняться 0.975 или 0.025, так как это двусторонний тест) и суммарную степень свободы – сумма степеней свободы выборок.
dfs = (half - 1) + (half - 1) scipy.stats.t.ppf(0.975, dfs).
В результате получили:
1.9605323551806582
что превышает вычисленное значение t-статистики — 1.556. Это означает, что мы не можем отвергнуть нулевую гипотезу. Отсюда заключаем: средние двух выборок равны при условии их нормального распределения.
Линейная регрессия в Statsmodel
Если необходимо оценить связь между двумя атрибутами или более, можно использовать линейную регрессию. Например, с возрастанием одного атрибута увеличивается значение второго или наоборот. Python имеет библиотеку statsmodel, предоставляющую классы и функции для оценки статистических моделей [3].
Линейную регрессию можно построить с помощью метода наименьших квадратов. В statsmodel есть API, который дает возможность писать в R-стиле. Например, рассмотрим Rings, количество колец, и Diamеter, диаметр моллюска:
import statsmodels.formula.api as smf
model = smf.ols('Rings ~ Diameter', data=data)
res = model.fit()
Метод ols принимает в качестве аргументов формулу для вычислений и DataFrame. summary вернет результат вычисленной модели:
res.summary()
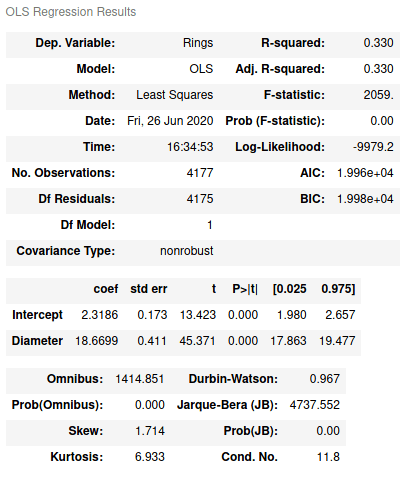
Как видим, здесь имеется широкий перечень статистических критериев: R2, F-статистика, коэффициенты линейного уравнения (Intercept и Diameter), степень свободы (Df model) и т.д. Например, R2 показывает 0.33, что значит только 33 % атрибута Rings может быть объяснено атрибутом Diameter.
Как известно, условием построения линейной регрессии является нормально распределенные остатки [4]. Чтобы получить остатки, используется атрибут resid:
>>> res.resid 0 5.866905 1 -0.266103 2 -1.159940 3 0.866905 4 -0.079403 ... 4172 0.279962 4173 -0.533339 4174 -2.186786 4175 -1.373485 4176 -0.680380 Length: 4177, dtype: float64
Отметим, что для построения линейной регрессии по двум независимым переменным формула бы выглядела так ‘Rings ~ Diameter + Height’.
Примеры кода выложены на github. В следующей статье мы поговорим об использовании лямбда-функций в Python. А подробные нюансы использования статистических Python-функций и модулей для применения в реальных проектах Data Science вы узнаете на наших курсах в лицензированном учебном центре обучения и повышения квалификации ИТ-специалистов в Москве.
- https://en.wikipedia.org/wiki/Shapiro%E2%80%93Wilk_test
- https://ru.wikipedia.org/wiki/%D0%9A%D1%80%D0%B8%D1%82%D0%B5%D1%80%D0%B8%D0%B9_%D1%81%D0%BE%D0%B3%D0%BB%D0%B0%D1%81%D0%B8%D1%8F_%D0%9F%D0%B8%D1%80%D1%81%D0%BE%D0%BD%D0%B0
- https://www.statsmodels.org/stable/index.html
- http://statistica.ru/theory/osnovy-lineynoy-regressii/