10 алгоритмов машинного обучения, которые нужно знать в 2021

Не секрет, что в мире Data Science имеется огромное количество алгоритмов машинного обучения (Machine Learning). Но какие нужно знать и понимать хотя бы на концептуальном уровне. В этой статье мы расскажем о 10 передовых и актуальных алгоритмов машинного обучения и приведем краткую информацию о характеристиках, начиная с линейной регрессии, ансамблевых методов и заканчивая бустинговыми решениями.

Линейная регрессия

Линейная регрессия (Linear regression) — один из самых фундаментальных алгоритмов, используемых для моделирования отношений между зависимой переменной и несколькими независимыми переменными. Целью обучения является поиск линии наилучшего соответствия.

В процессе обучения линейной регрессии находится минимизация квадратов расстояний между точками и линией наилучшего соответствия. Этот процесс известен как минимизация суммы квадратов остатков. Остаток равен разности между предсказанным значением и реальным.

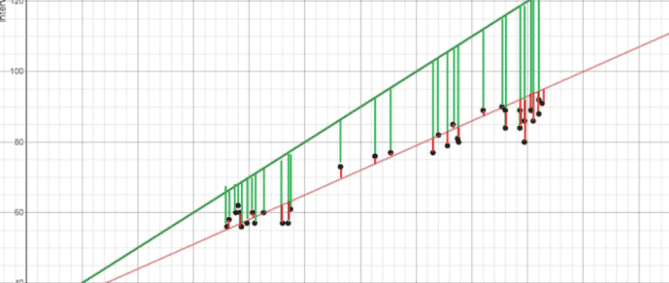
О линейной регрессии можно узнать тут.

Логистическая регрессия

Логистическая регрессия (Logistic regression) похожа на линейную регрессию, но используется для моделирования вероятности дискретного числа результатов, обычно двух. Несмотря на то что в название алгоритма входи слово «регрессия», он используется для задачи классификации.

В основе принципа работы логистической регрессии лежит то же уравнение, что и в линейной регрессии. Но добавляется дополнительный шаг в виде использования сигмоидальной функции, которая возвращает вероятность похожести с целевым значением. Для расчёта весов применяются методы градиентного спуска или максимального правдоподобия.

Метод k-ближайших соседей

Метод k-ближайших соседей (k-nearest neighbors) — это очень простой алгоритм машинного обучения. Все начинается с данных, которые уже классифицированы (т.е. красные и синие точки данных). Затем при добавлении новых точек, алгоритм классифицируете её, просматривая k ближайших классифицированных точек. Какой класс наберёт больше всего голосов определяет, как будет классифицироваться новая точка.

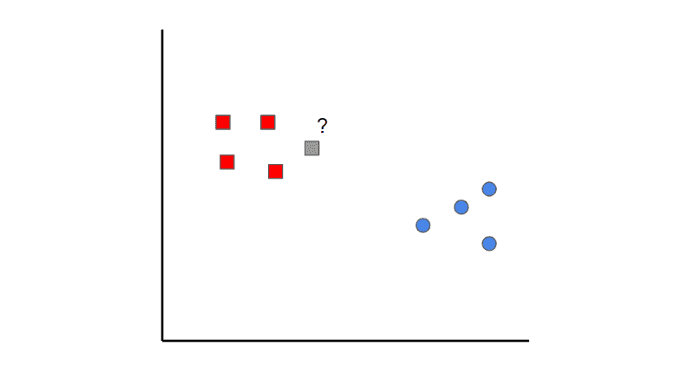
Например, рассмотрим рисунок выше. Если мы определим k = 1, мы увидим, что первая ближайшая точка к серому образцу — это красный квадрат. Следовательно, точка будет классифицирована как красная. Хотя такой же результат будет и при k = 2.

Следует иметь в виду, что если значение k установлено слишком низким, оно может иметь выбросы. С другой стороны, если значение k установлено слишком высоким, то классы с несколькими выборками могут быть пропущены.

Наивный байесовский классификатор

Наивный байесовский классификатор (Naive Bayes classifier) может вводить в ступор, поскольку он требует предварительных математических знаний в области условной вероятности и теоремы Байеса, но это очень простой алгоритм.

Предположим, что имеются данные погодных условий, при которых человек шёл или не шёл играть в гольф.

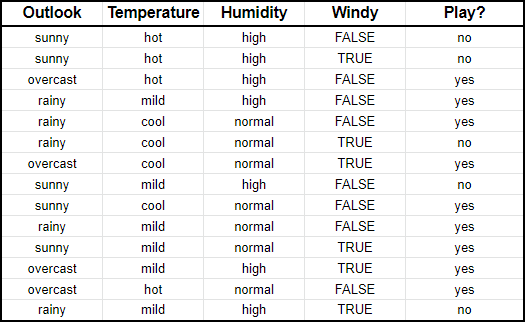
Наивный байесовский классификатор сравнивает соотношение между каждой входной переменной и категориями выходной переменной. Это можно увидеть в таблице ниже. Например, вы можете заметить, что в столбце с температурой было жарко в течение двух дней из девяти дней, когда человек играл в гольф.

В математических терминах это записывается как вероятность того, что человек шёл играть в гольф при каких-то условиях, и обозначается как P(yes|<условие>). Это нотация называется условной вероятностью. В алгоритме всего лишь нужно посчитать всевозможные условные вероятности.

Допустим, что имеются следующие характеристики:

• Outlook: sunny
• Temperature: mild
• Humidity: normal
• Windy: false

Нужно вычислить вероятность того, что вы человек пойдёт играть в гольф при этих погодных условиях, то есть рассчитать P(yes|X), а затем вероятность того, что человек не пойдёт играть P(no|X). Из таблицы выше мы знаем, что

   

   

   

   

   

Теперь мы можем просто посчитать условную вероятность

   

   

   

Аналогично рассчитывается вероятность того, что человек не пойдёт (т.е. вместо yes будет no):

   

Поскольку , то наивный байесовский классификатор говорит, что этот человек пойдет играть в гольф, учитывая солнечную погоду, умеренную температуру, нормальную влажность и безветренность.

Метод опорных векторов

Метод опорных векторов (Support Vector Machine) применяется во многих задачах, и с математической точки зрения может быть сложным, но довольно интуитивно понятным на концептуальном уровне.

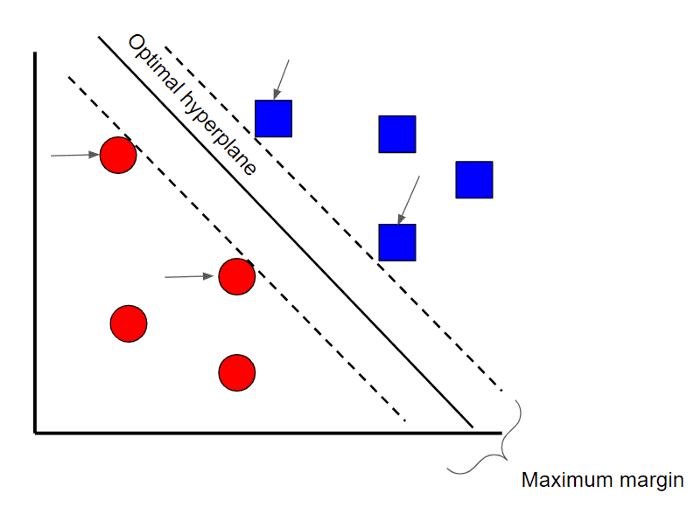
Предположим, что есть два класса данных. В основе метода опорных векторов лежит нахождение гиперплоскости (границу между двумя классами данных), которая максимизирует разницу между двумя классами. Есть много плоскостей, которые могут разделять два класса, но только одна плоскость истинная.

Деревья решений

Деревья решений (Decision trees) — это непараметрический контролируемый метод обучения, используется для задачи классификации и регрессии. Цель состоит в том, чтобы создать модель, которая предсказывает значение целевой переменной, изучая простые правила принятия решений, выведенные из характеристик данных. Дерево можно рассматривать как кусочно-постоянное приближение. Концептуально деревья решений очень понятный алгоритм, что достаточно одной схемы, чтобы понять его принцип работы.

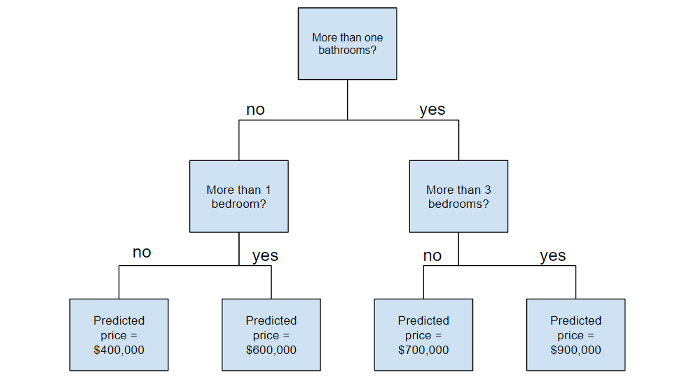
Случайный лес

Случайные леса (Random Forest) — это метод ансамблевого обучения, основанный на деревьях решений. Случайные леса включают создание нескольких деревьев решений с использованием самонастраиваемых наборов исходных данных и случайного выбора подмножества переменных на каждом шаге дерева решений. Затем модель собирает пакет прогнозов каждого дерева решений. Модель считает количество прогнозов «за» и «против» и выносит решение, исходя из большинства голосов.

AdaBoost

AdaBoost, или адаптивный бустинг, также представляет собой ансамблевый алгоритм, который использует методы сбора прогнозов и подсчета голосов. AdaBoost похож на случайные леса в том смысле, что прогнозы берутся из многих деревьев решений. Однако есть три основных отличия:

1. В AdaBoost используются деревья с одной вершиной и двумя узлами.
2. Не все создаваемые деревья имеют право голоса для окончательном прогноза. Те, которые часто ошибались, будут меньше влиять на окончательное решение.
3. Порядок расположения деревьев важен. Прогнозы дерева направлены на уменьшение ошибок, сделанных предыдущими.

Gradient Boost и XGBoost

Ещё один ансамблевый алгоритм Gradient Boost (градиентый бустинг) похож на AdaBoost, но у него есть несколько ключевых отличий:

• Gradient Boost строит деревья до 32 узлов.
• Gradient Boost рассматривает проблему оптимизации, где он использует функцию потерь и пытается минимизировать ошибку с помощью градиентного спуска.
• Деревья используются для прогнозирования остатков (разница между предсказанными и реальными данными, т.е. ошибки).

Алгоритм Gradient Boost начинается с построения одного дерева, а последующие деревья нацелены на уменьшение остатков.

XGBoost — один из самых популярных и широко используемых алгоритмов, который основан на градиентном бустинге. К характеристикам XGBoost относятся:

• Newton Boosting обеспечивает путь к глобальному минимуму быстрее, чем градиентный спуск
• Дополнительный параметр рандомизации — уменьшает корреляцию между деревьями, в конечном итоге улучшая предсказательную силу

Вы можете ознакомиться с алгоритмом на странице с документацией библиотеки XGBoost (Python API также доступен), где также объясняется и Gradient Boost

LightGBM

Помимо XGBoost, есть ещё один ансамблевый алгоритм LightGBM. Что отличает LightGBM, так это то, что он использует метод, называемый односторонней выборкой на основе градиента (Gradient-based One-Side Sampling), чтобы отфильтровать данные и найти точку разделения между данными. Этим он отличается от XGBoost, который использует предварительно отсортированные и основанные на гистограммах алгоритмы для поиска лучшего разделения.

 

Еще больше подробностей о вышеприведённых алгоритмах машинного обучения, а также их применение для разных практических задач Data Science, включая задачи регрессии, классификации и кластеризации, вы узнаете на нашем специализированном курсе «PYML: Введение в машинное обучение на Python» в лицензированном учебном центре обучения и повышения квалификации Data Scientist’ов и IT-специалистов в Москве.

1. https://xgboost.readthedocs.io/en/latest/python/index.html