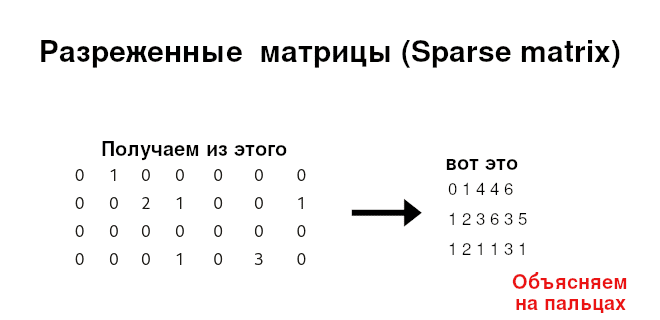
В одной из статей по Apache Spark я говорил о разреженных (sparse) матрицах, но не вдавался в подробности. Многих сбивают с толку эти разреженные матрицы, поскольку формат их хранения отличается от плотных матриц. Тем не менее, разреженные матрицы очень часто используются в Data Science, поскольку их хранение менее затратное. Сегодня мы шаг за шагом рассмотрим переход от плотных матриц к разреженным, начав со списка координат (COOrdinate list) и закончив сжатым хранением строкой (CSR) и столбцом (CSC).
Локальные векторы: плотные и разреженные
Допустим, что у нас имеется матрица (см. рисунок ниже). При беглом взгляде осознаем, что в ней много нулей (возможно, это матрица c категориальными значениями) А что если бы это была матрица 1000×1000? А матрица 100000×500000 со всеми этими нулями? Нет смысла хранить матрицу, где большая часть элементов – это нули. Поэтому пришли к так называемым разреженным матриц (sparse matrix).
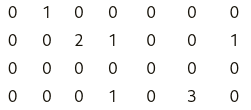
Разреженные матрицы представляют в различных форматах:
- координатный список (Coordinate List),
- сжатое хранение строкой (Compressed Sparse Row),
- сжатое хранение столбцом (Compressed Sparse Column),
- список списков (List of lists),
- словарь ключей (Dict of keys)
Мы расскажем о первых трех, так как они встречаются чаще.
Список координат (Coordinate List)
Возможно, самый очевидный формат хранения разреженных матриц является список координат. Такой формат представляет собой триплет (строка, столбец, значение). При этом, хранятся только ненулевые значения. Например, матрицу выше можно записать следующим образом:

В этом формате еще хранится размерность матрицы. Подразумевается, что не записанные значения являются нулями.
Улучшаем, применив правило row-major order
Мы можем еще улучшить список координат. Давайте вместо того чтобы хранить каждый индекс строки, будем хранить количество ненулевых значений на каждой строке. Вот, что случится, после применения данного правила:

Подобное правило примененное к строкам называется порядок по строкам (row-major mode). Ничто не мешает применить его к столбцам, тогда это будет порядок по столбцам (column-major order) [1].
Как можно заметить, теперь мы храним меньше данных: в данном примере меньше на два элемента по сравнению с оригинальным списком координат.
А что насчет компьютера? Получается, что он хранит три массива и размерность разреженной матрицы. Тогда как извлечь отдельные строки (поскольку это row-major order) из нее? Алгоритм извлечения p-й строки достаточно прост. Допустим, нам нужна 3-я строка (не забываем про счет с 0), т.е. последняя строка (0,0,0,1,0,3,0), тогда требуется:
- Определить количество n ненулевых элементов выше p-й строки. Выполнить эту процедуру путем суммирования элементов в векторе
Не-0 в строкевплоть до p-й строки. Для 3-й строки получается 1 + 3 + 0 = 4, значит количество ненулевых элементов выше 3-й строки равно 4. - Определить количество k элементов в p-й строке. Это значение равно p-му элементу вектора
Не-0 в строке. Для 3-е строки это значение равно 2. - Дойти до элемента n + 1 векторов
СтолбециЗначение. В нашем случае это 4 + 1 = 5. - Взять k пар элементов векторов
СтолбециЗначение. В нашем случае это пары(3, 1)и(5, 3). - Вернуть вектор размера N (где N – это количество строк) с заполненными соответствующими парами, а остальные элементы заполняются нулями. В нашем случае это
a[3] = 1иa[5] = 3, а все остальное — это нули.
Сжатое хранение строкой (Compressed Sparse Row, CSR)
А что если мы захотим извлечь строку 2-ю, потом 1-ю, потом снова 2-ю и т.д. Исходя из алгоритма, происходит суммирование элементов вектора Не-0 в строке каждый раз при извлечение очередной строки. Так, может быть, сразу и заменим вектор Не-0 в строке на кумулятивную сумму количества ненулевых элементов в строке и назовем новый вектор Кумулята Не-0 в строке. Тогда получится такой результат:

И вот снова требуется получить p-ю строку, например, 3-ю. Тогда алгоритм ее получения будет следующим:
- Определить количество ненулевых элементов выше p-й строки. Это просто (p — 1)-й элемент вектора
Кумулята Не-0 в строке. Для 3-й строки — это 4. - Определить количество ненулевых элементов в строке p. Это количество равно разнице между p-м и (p-1)-м элементами вектора
Кумулята Не-0 в строке. Для 3-й строки эта разница между 3-м и 2-м элементами, т.е. 6 — 4 = 2. - Шаги 3, 4, 5 такие же, как и выше.
В первом шаге нужно добавить условие при извлечении 0-ю строки: Если требуется 0-я строка, вернуть 0 — поскольку выше этой строки ничего нет.
Такой формат хранения называется сжатое хранение строкой (Compressed Sparse Row, CSR).
Сжатое хранение столбцом (Compressed Sparse Column, CSC)
В задачах машинного обучения (machine learning) наиболее распространенной практикой является извлечение столбцов (признаков) нежели строк. С точки зрения математики строки и столбцы матрицы эквивалентны, поэтому правила выше можно применять к столбцам. Такая форма представления называться сжатое хранение столбцом (Compressed Sparse Column, CSC).
Если мы будем считать кумуляту по столбцам, т.е. по правилу порядка по столбцам (column-major order), то получим следующее:

При извлечении столбца считаем то, что левее и правее необходимого. И также возвращается 0 на первом шаге алгоритма при извлечении 0-го столбца.
Еще больше подробностей о векторах, матрицах и других структурах данных с примерами из Data Science вы узнаете на специализированном курсе по машинному обучению «PYML: Введение в машинное обучение на Python» в лицензированном учебном центре обучения и повышения квалификации разработчиков, менеджеров, архитекторов, инженеров, администраторов, Data Scientist’ов и аналитиков Big Data в Москве.